En este caso os dejo los apuntes maravillosos que he encontrado en una página que además os servirá para ver exámenes y buscar información que no os haya quedado clara o para ampliar conocimientos. Gracias a 10endibujo por compartir su buen hacer.
LA CIRCUNFERENCIA COMO ELIPSE EN PERSPECTIVA ISOMÉTRICA. TRAZADO POR 2 MÉTODOS Y DIFERENCIAS CON EL ÓVALO
La elipse es la figura exacta que representa la circunferencia en Perpectiva Isométrica.
En este artículo vas a aprender a dibujarla de dos maneras diferentes y vas a conocer las diferencias de trazado con respecto al óvalo.
Durante décadas ha servido el óvalo de manera oficial como representación de la circunferencia en isométrica. De hecho, fue el sistema que yo aprendí en el año 99 y que puedes ver de manera detallada aquí.
No obstante, en las últimas semanas he recibido mensajes de varios profesores de dibujo técnico de secundaria (mil gracias a todos por vuestra generosidad y por mantenerme al día) diciendo que ahora se exige en selectividad dibujar la circunferencia como elipse en perspectiva isométrica.
Por tanto, vamos a ver cómo se dibuja la elipse de manera precisa.
1. LA CIRCUNFERENCIA COMO ELIPSE EN ISOMÉTRICA
Para dibujar una circunferencia en Perspectiva Isométrica ya sea con un método o con otro, lo primero que necesitamos es tener:
- Los ejes isométricos, que forman 120º entre sí, como sabes de este artículo de axonometrías)
- El cuadrado que circunscribe la circunferencia, es decir, el cuadrado en el que la circunferencia va a estar inscrita. Este cuadrado debe tener los 4 lados de la misma dimensión, que es igual a la dimensión del diámetro ∅.
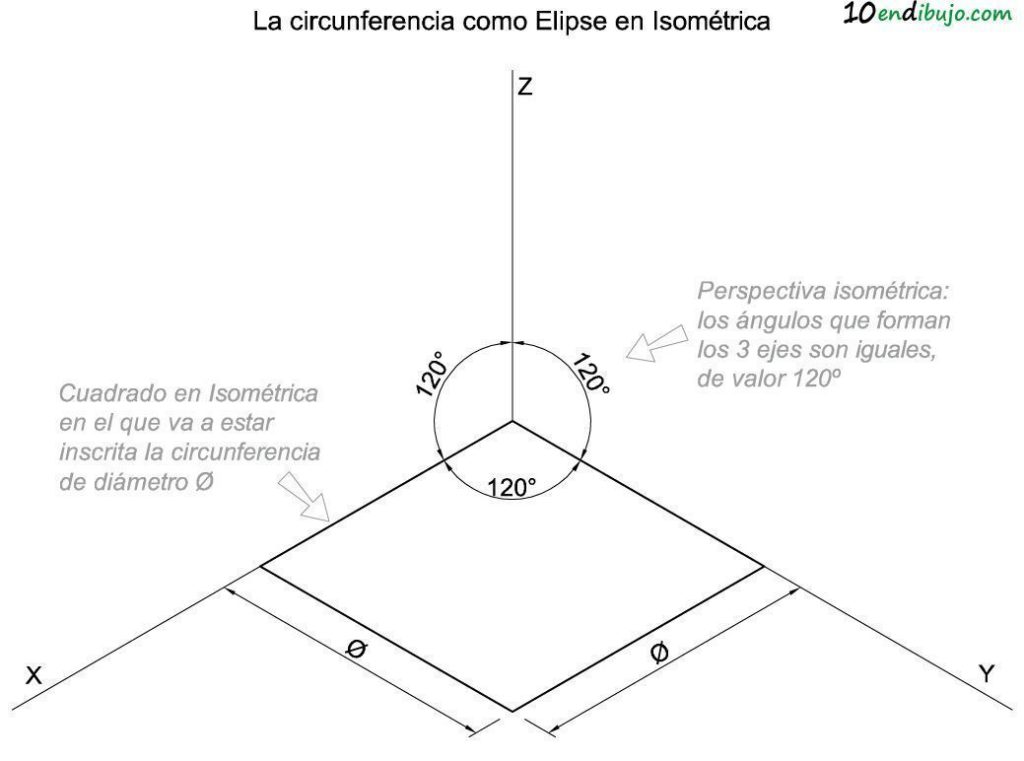
Obviamente la dimensión del cuadrado debe estar acorde con la escala que te pidan y el coeficiente de reducción correspondiente si es que tienes que aplicarlo (puedes verlo aquí explicado).
Por el momento vamos a dibujar la circunferencia únicamente en el plano horizontal, el formado por los ejes X e Y.
Y vamos a dibujar esa elipse utilizando 2 métodos diferentes.
1.1. LA ELIPSE EN ISOMÉTRICA POR AFINIDAD
Este es el método más sencillo y el que menos líneas necesita.
Es bastante similar a la manera de dibujar la circunferencia en Perspectiva Caballera, por lo que si ya conoces ese método, este te resultará muy sencillo.
Básicamente consiste en los siguientes pasos:
- Dibujar un cuadrado en verdadera magnitud cuyo lado coincida con uno de los lados del cuadrado en perspectiva. Ese lado representa el Eje de Afinidad, también conocido como recta de puntos dobles, si recuerdas de afinidad
- Dibujar la circunferencia inscrita en el cuadrado anterior. El centro O’ de dicha circunferencia se encuentra en la intersección de las diagonales del cuadrado. Para conocer el radio es necesario dibujar una recta perpendicular a uno de los lados del cuadrado desde el centro O’ de la circunferencia.
- Dibujar la elipse afín de la circunferencia. Los puntos A’, B’, C’ y D’ son los afines de los extremos de los ejes de la elipse. Solo hay que encontrar sus afines A, B, C y D; teniendo los ejes de una elipse, ya se puede dibujar de manera precisa.
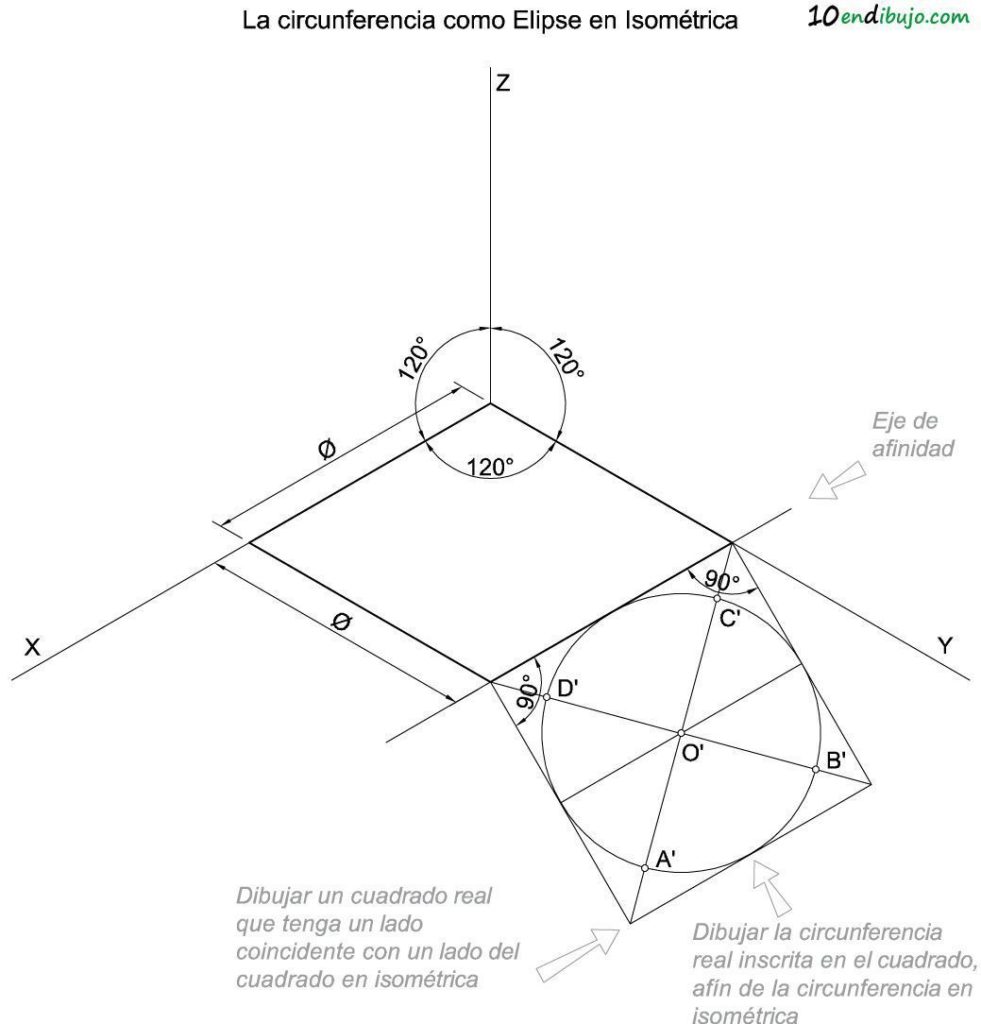
Para encontrar esos ejes de la elipse afines debemos encontrar el centro O de la circunferencia en perspectiva isométrica, que se encuentra en la intersección de las diagonales en isométrica.
Ese punto O es afín del centro O’.
El eje de afinidad y el par de puntos afines O y O’ definen completamente la afinidad.
En cualquier caso, los lados del cuadrado real son afines a los lados del cuadrado en perspectiva. Y si recuerdas de afinidad, dos rectas paralelas tienen rectas afines paralelas. Por tanto las rectas A’-D’ y B’-C’ (que son paralelas a los lados del cuadrado) tienen sus afines en rectas paralelas a los lados del cuadrado en perspectiva: A-D y B-C.
Por tanto solo hay que prolongar las rectas A’-D’ y B’-C’ hasta el Eje de Afinidad y desde allí dibujar paralelas al Eje Y para encontrar los puntos A, B, C y D sobre las diagonales.
Los segmentos A-C y B-D son los ejes de la elipse.
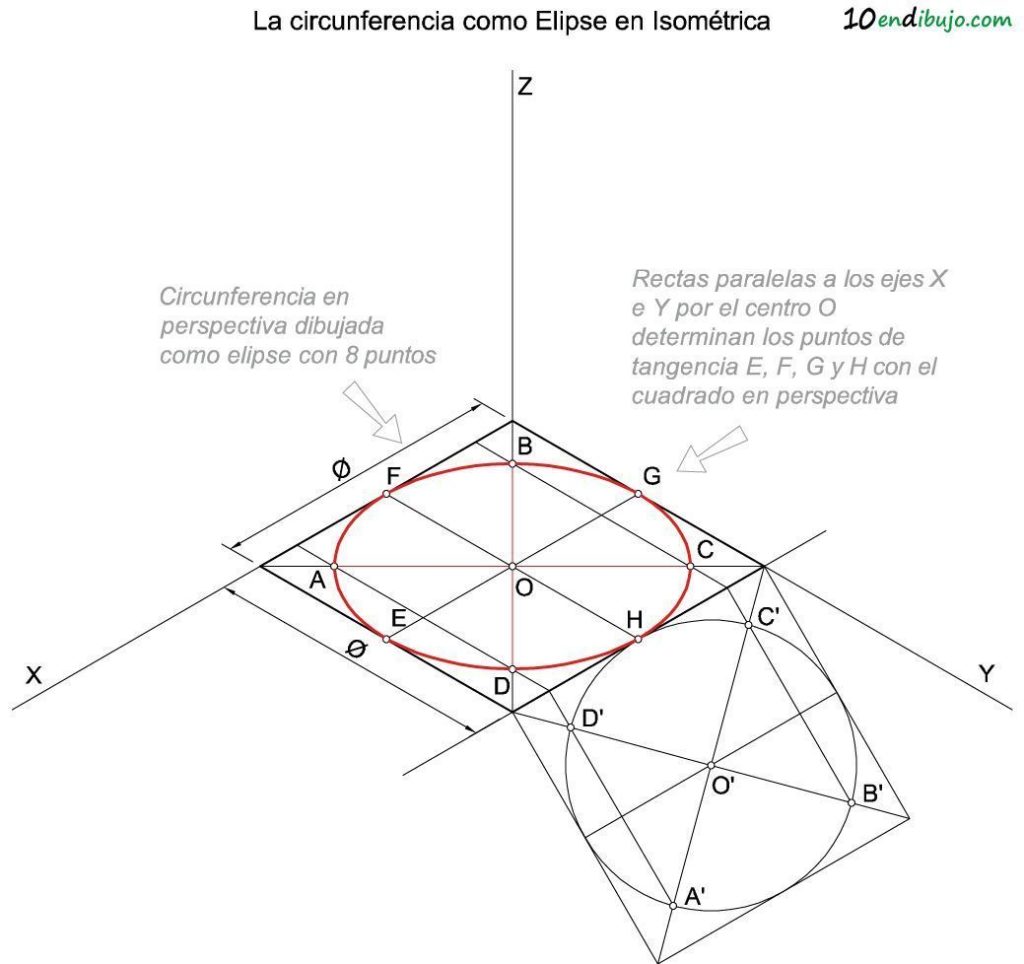
Para dibujar la circunferencia como elipse en el plano X-Z puedes emplear cualquiera de los dos métodos siguientes:
- Utiliza el eje X como eje de simetría. Si ya tienes dibujada la circunferencia en el plano XY es sencillo dibujar las diagonales del cuadrado en perspectiva en el plano XZ y obtener los puntos 1, 2, 3 y 4, que sean simétricos de A, B, C y D. Observa que las rectas B-C y A-D son simétricas de 2-3 y 1-4 respectivamente.
- Aplica el mismo proceso que para el plano XY. Si no te ha hecho falta dibujar la elipse en el plano XY, lo más sencillo es que apliques el método explicado anteriormente a este plano. Para ello, dibuja el cuadrado en verdadera magnitud con un lado coincidente con el cuadrado en perspectiva. Dibuja seguidamente la circunferencia y las diagonales del cuadrado y encuentra por último los puntos afines de 1′, 2′, 3′ y 4′.
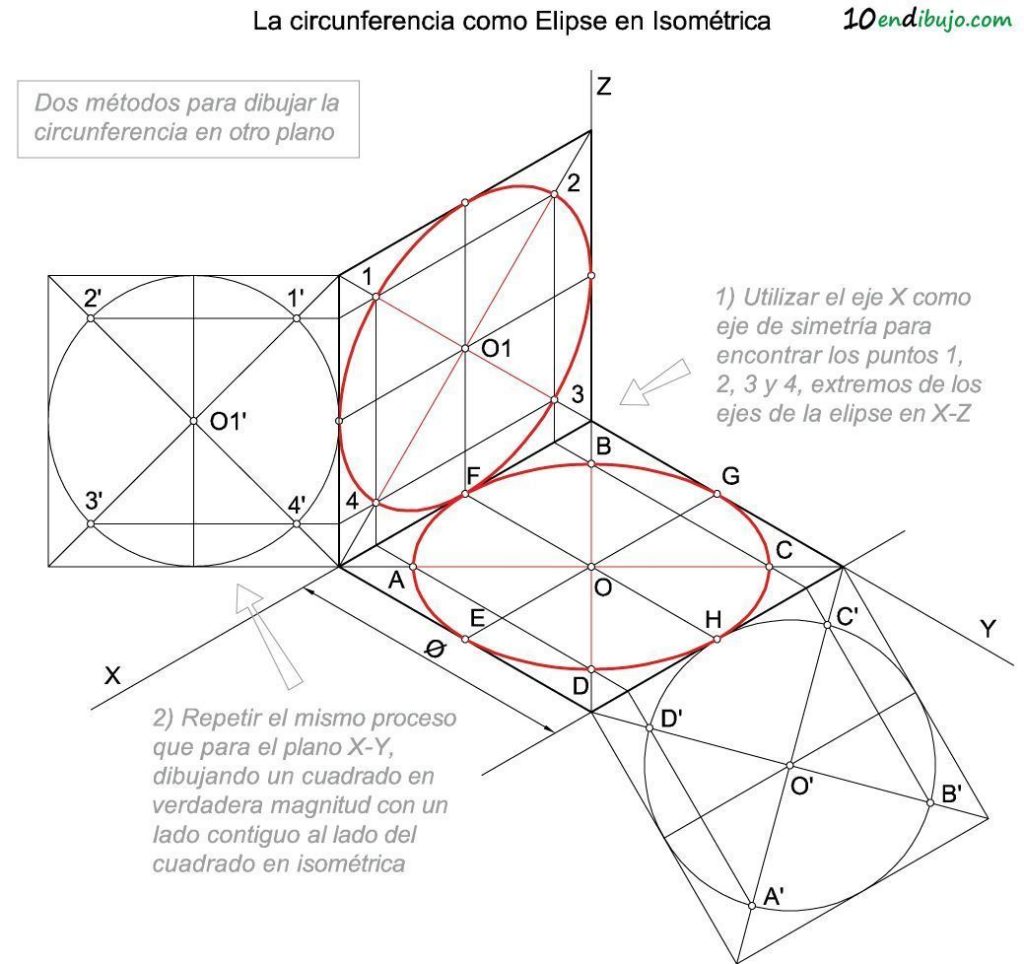
Considero que el método explicado para dibujar la elipse en isométrica mediante afinidad es el más sencillo e inmediato, pero no es el único.
Si sabes cómo funciona el Sistema Axonométrico, apuesto a que el siguiente método también te parece útil.
De todas formas, si lo único que buscabas era resolver la circunferencia como elipse en isométrico, con lo visto hasta ahora tienes suficiente. El resto son métodos alternativos y otras observaciones que pueden resultar interesantes para quien quiera profundizar y entender conceptos nuevos de dibujo técnico.
1.2. LA ELIPSE EN ISOMÉTRICA POR ABATIMIENTO
Según explicamos en este artículo, cuando trabajamos en perspectiva isométrica, estamos trabajando con una Axonometría con una determinada posición de los ejes, en la cual los ejes forman 3 ángulos iguales de 120º.
Observa en este dibujo extraído directamente de aquel artículo cómo, cuando trabajamos en perspectiva, en realidad estamos dibujando sobre el Plano del Cuadro.
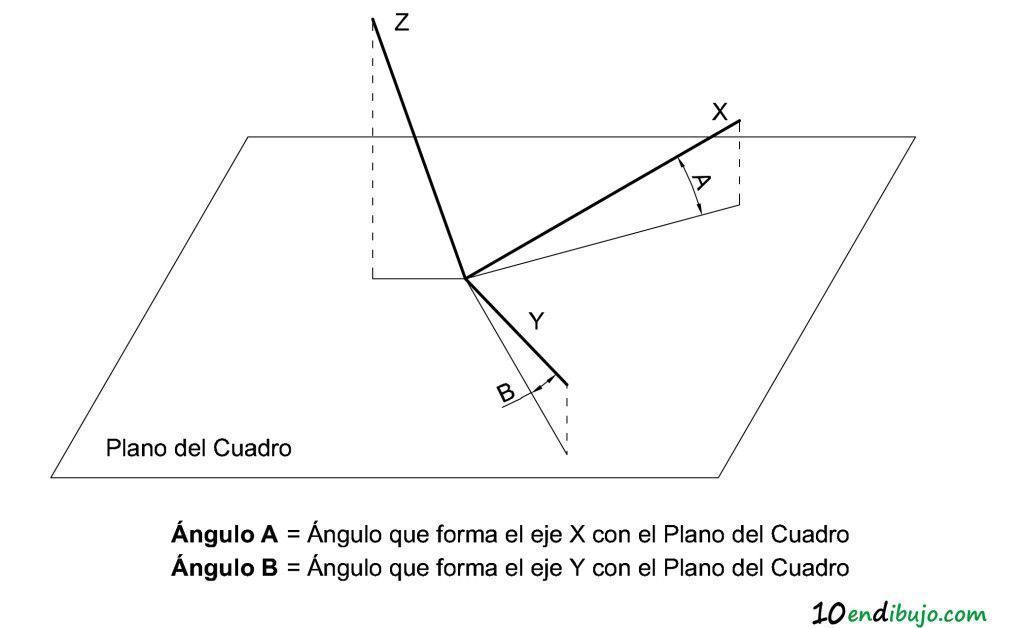
Pues bien.
Lo que vamos a hacer en este método es abatir sobre el Plano del Cuadro.
O más concretamente, vamos a abatir sobre un plano paralelo al Plano del Cuadro.
Si consigues visualizarlo en el espacio, la intersección del plano XY con el Plano del Cuadro es una recta perpendicular a Z que pasa por el centro de coordenadas.
Nosotros utilizaremos como charnela de abatimiento una recta paralela a esta que pase por el vértice opuesto del cuadrado en perspectiva.
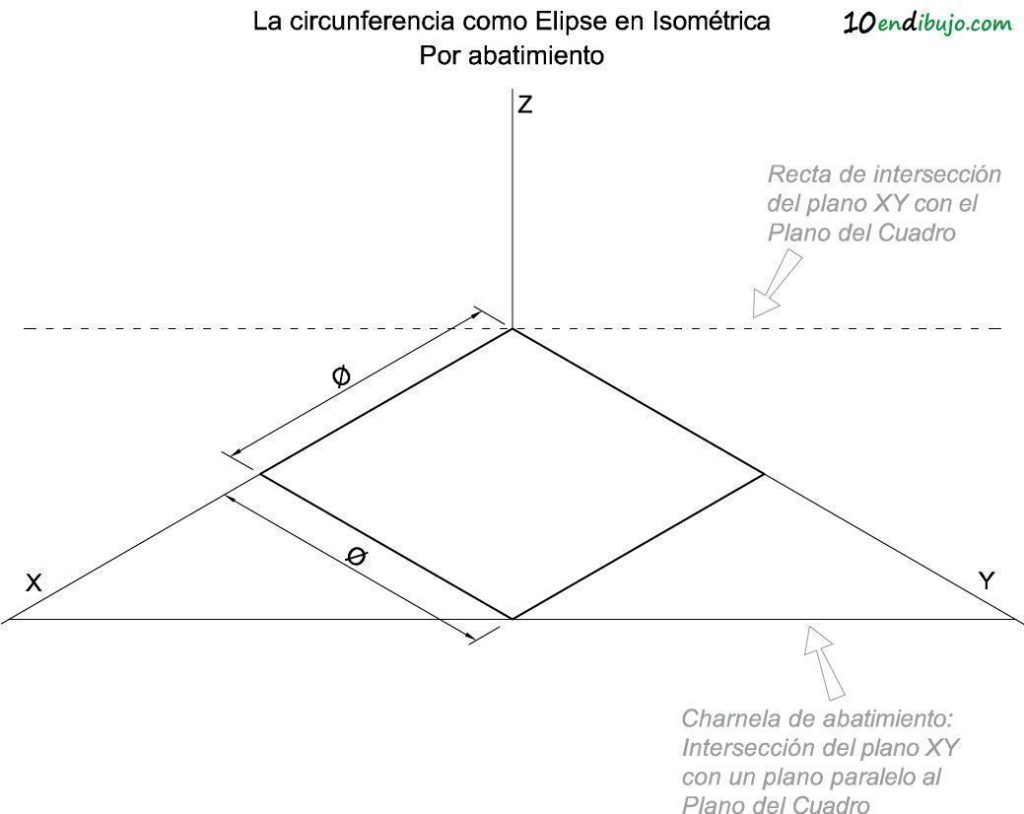
ABATIMIENTO DEL CENTRO DE COORDENADAS
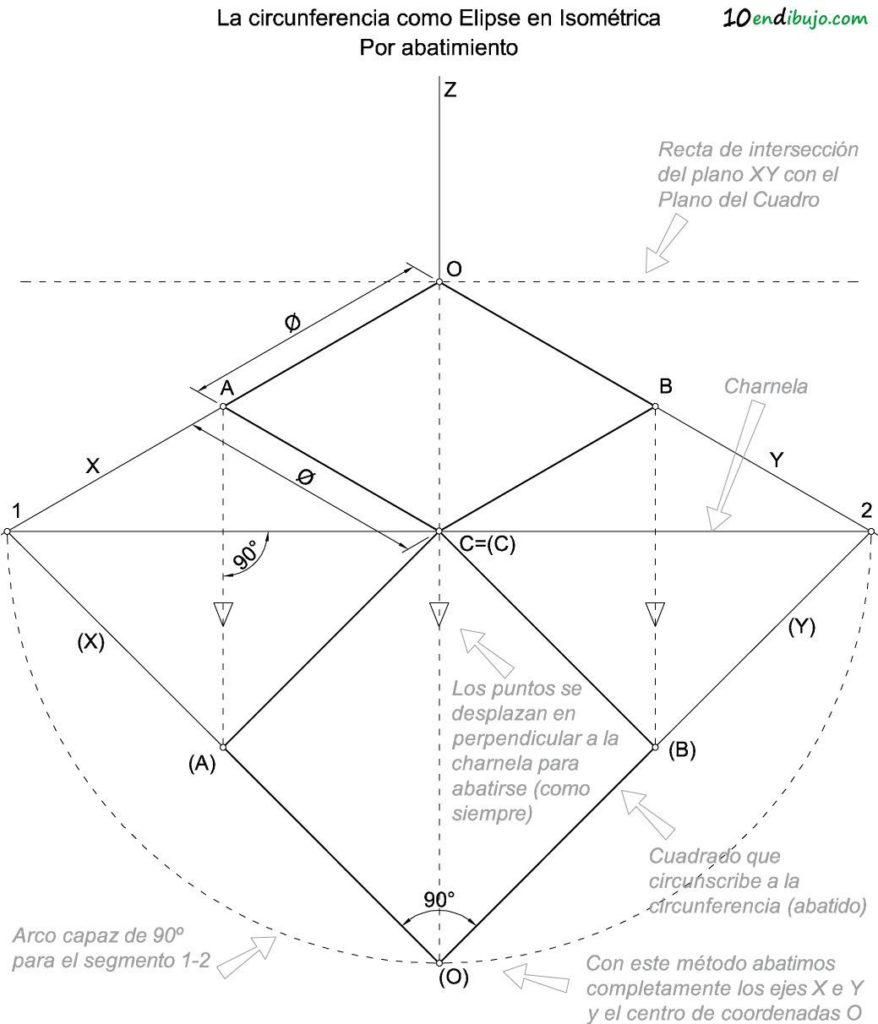
Puesto que sabemos que los ejes X e Y forman un ángulo en la realidad de 90º en el centro de coordenadas, solo tenemos que dibujar un arco capaz de 90º para el segmento 1-2.
Y también sabemos que los puntos se desplazan en perpendicular a la charnela para abatirse.
De esta manera se consigue el punto (O), que es el abatimiento del centro de coordenadas O.
ABATIMIENTO DEL CUADRADO CIRCUNSCRITO A LA CIRCUNFERENCIA
Al unir (O) con 1 y con 2 obtenemos los ejes (X) e (Y) abatidos (que obviamente forman un ángulo recto entre sí en verdadera magnitud).
Quedaría desplazar los puntos A y B hasta su posición (A) y (B) en abatimiento sobre los ejes (X) e (Y).
Por último, puesto que el punto C pertenece a la charnela, su abatido (C) coincide con él.
De esta manera conseguimos cerrar el cuadrado que circunscribe a la circunferencia, ya en verdadera magnitud en el abatimiento.
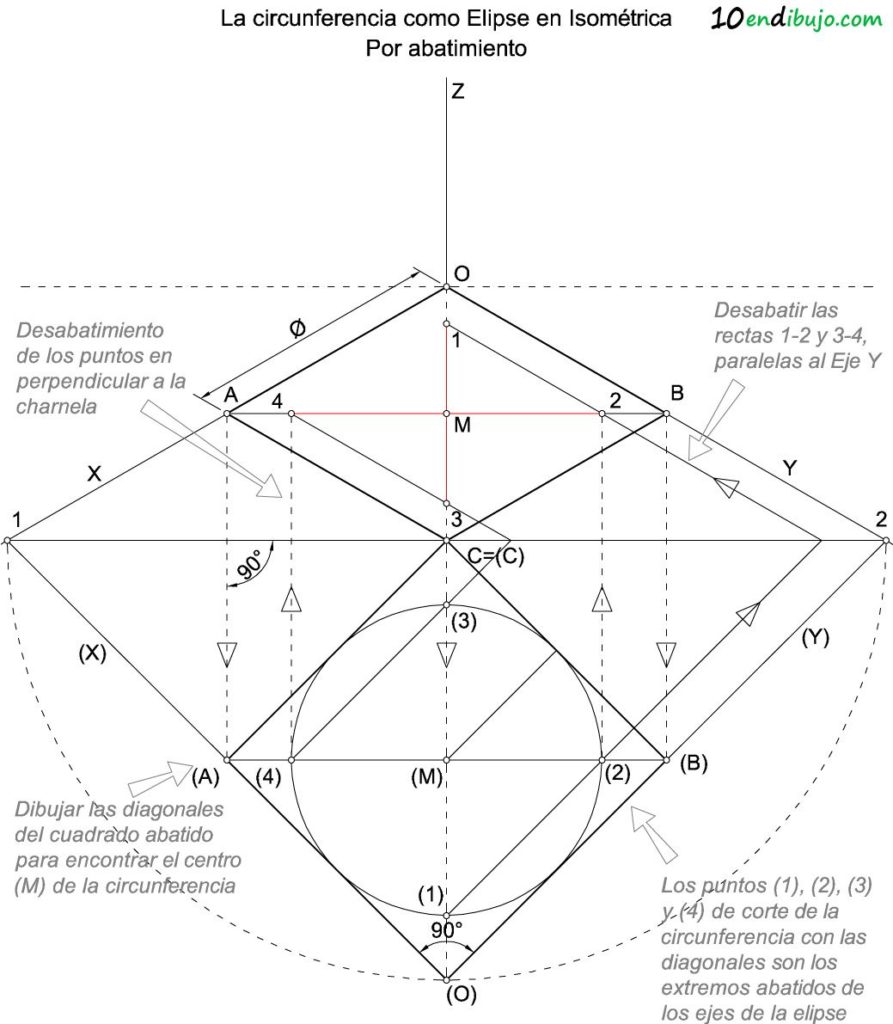
Una vez que tenemos el cuadrado abatido, podemos dibujar la circunferencia inscrita, dibujando las diagonales para encontrar el centro (M) y trazando desde este centro una perpendicular a uno de los lados para conocer su radio.
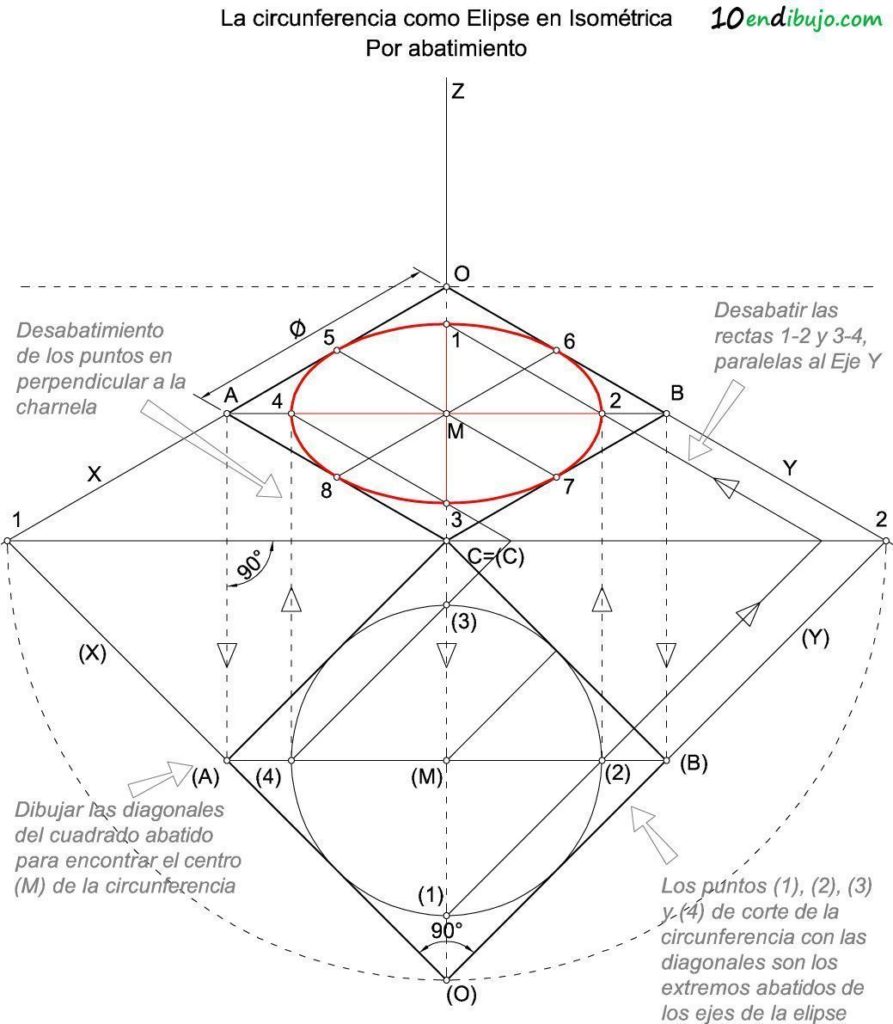
Los puntos (1), (2), (3) y (4) donde la circunferencia corta a las diagonales son los extremos abatidos de los ejes de la elipse. Observa que simplemente trazando perpendiculares a la charnela desde (2) y (4) puedes encontrar los puntos 2 y 4 desabatidos sobre las diagonales del rombo (cuadrado en perspectiva isométrica).
También puedes desabatir las rectas (1)-(2) y (3)-(4).
Solo tienes que prolongarlas hasta la charnela y desde ahí dibujar las rectas paralelas al eje Y hasta que corten las diagonales en los puntos 1, 2, 3 y 4.
Los segmentos 1-3 y 2-4 son los ejes de la elipse.
Con esto ya estamos en la misma situación que en el apartado anterior: dibujar una elipse dados los dos ejes ortogonales.
Como decíamos antes, hay diferentes métodos para dibujar la elipse con estos datos. Para nuestro caso, lo más sencillo, preciso y recomendable es encontrar los puntos de tangencia con el cuadrado en perspectiva.
Para ello solo tienes que dibujar rectas paralelas a los ejes X e Y desde el centro M y esto nos dará los puntos 5, 6, 7 y 8.
Con un total de 8 puntos es fácil dibujar a mano alzada una elipse.
Este segundo método para dibujar la elipse en perspectiva isométrica ocupa más espacio en el papel y tengo la impresión de que necesita algo más de líneas, por lo que yo diría que es menos recomendable que hacerlo por afinidad.
Aun así, no quería desaprovechar la ocasión para presentar este método para que lo aprendieran y entendieran quienes quieren profundizar en el Dibujo Técnico, especialmente aquellos interesados en el Sistema Axonométrico.



